심볼릭 파이선에서 다음과 같은 기능을 테스트 해보려고 했는데 에러가 발생하였다. 처음 시도해보려는 예제에서부터 문제가 발생해서 당황해서 나에게 문제가 있나? 하고 매트랩에서 실행을 해보았으나 정상적으로 수행이 되었다.
symbolic python을 잠깐 사용했을 때 이정도까지 되는건가? 하고 신기했는데 가장 간단하게 생각되는 부분에서 막혀서 약간 맥이 빠진 느낌이다.
우선 사용자가 원하지 않는데 단순화를 진행하는 것이다. 다음은 symbolic python의 라이브 에디터의 출력 결과이다. tan (x-pi/2)의 형태를 보고 싶은데 친절하게도 이미 변환된 결과를 출력해준다.

다음은 매트랩의 결과이다. simplify 명령어를 통해서 간략화한 결과를 확인할 수 있다.

그럼 symbolic python은 simplify 명령어가 없냐고? 엄연히 존재한다;;;;;
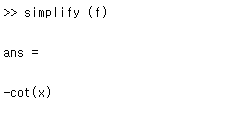
다음의 경우 tan 함수의 결과는 +0 에서 음수의 무한대, -0 에서는 양수의 무한대가 나와야한다.
\(\lim_{x \rightarrow +0} tan ( x – \frac{ \pi }{2} )
\)
다음은 매트랩에서의 양쪽 방향의 극한이다. 따라서 0이 특이점이라는 것을 확인할 수 있다.
symbolic python은 두가지 형태로 접근해볼 수 있다. Limit을 대문자로 작성할 경우에는 아래와 같이 표현형태로 저장된다. ( tan 문제는 여전히 존재한다!! ) 표현식일 경우 함수의 실행은 doit() 멤버함수를 호출하는 형식이다. limit을 소문자로 작성할 경우에는 즉시 결과값을 반환한다.

symbolic 연산을 제대로 할 수 있는 툴은 메이플이나 매스매티카 정도 였으나 (매트랩은 symbolic tool box를 또 돈주고 사야한다) 모두 상용이고 간단하게 결과를 확인해볼 수 있는 방법으로 울프럼 알파도 자주 사용하지만 아무래도 한계가 존재한다.
symbolic python을 처음보았을 때 0.xx 였었다. 이미 매트랩을 사용하고 있어 시간 지나면 사라지는 여러프로젝트중에 하나겠거니하고 신경을 끄고 있었는데 벌써 1.x로 정식버전이 나온지 좀 되었다. 문서들을 살펴보니 이제 좀 쓸만하구나라는 생각이 들고 활용 방법에 대해서 고민해봐야겠다.