electric potential (전위)는 – 책에서는 electrostatic potential 이라고 나와있는데 동일한 말이다 – 동일하다. 전위는 \( \Phi \) 의 함수로 나타낼 수 있으며 라플라스 방정식의 해이다.
\( \nabla^{2}\Phi = 0 \)equipotential surface (등전위면) 은 전위가 같은 지점을 선 또는 면으로 연결한 것이고 \( \Phi=상수 \) 가 된다.
어떤 지점 P에서 \( \Phi\)의 함수는 점 P와 등전위면을 통과하는 수직인 벡터 기울기 (gradient)를 나타낸 것이다. 전기장에서 등전위면은 전하가 작용하는 힘의 방향이 되기 때문이다. 여기까지가 책에서 다루는 내용이고 예제를 살펴보도록 한다.
전위를 띈 무한하게 펼쳐지 있는 판이 놓여져 있고 판이 y축에 각각 1, -1 의 위치에 있다고 할 경우 y=1에서의 potential 값을 \( \Phi_{1} \) 이라고 하고 y=-1의 위치에서는\( \Phi_{2} \) 이라고 하자.
\( \nabla^{2}\Phi = 0 \) 의 식을 편미분 방정식으로 나타낸다면 \(\nabla^{2}\Phi =\frac{\partial ^{^{2}} \Phi}{\partial x^{2}} +\frac{\partial ^{^{2}} \Phi}{\partial y^{2}}=0 \)이 된다.
이를 통해 \( \Phi\)의 함수는 \(\nabla^{2}\Phi\) 를 이차 적분을 할 경우 각각 미지수 a,b로하는 함수
\( \Phi_{1}(x,y)=ay+b \\ \Phi_{2}(x,y)=ay+b\) 로 정의할 수 있다. y=1인 경우와 y=-1에서의 값과 각 위치에서의 전위값을 함수에 대입한다면 \( \Phi_{1}(x,1)=ay+b=a+b=\Phi_{1} \\ \Phi_{2}(x,-1)=ay+b=-a+b=\Phi_{2}\) 가 된다.
이를 연립해서 풀 면 미지수 a,b는 전위 \( \Phi_{1}, \Phi_{2}\) 로 구성된 함수로 결정할 수 있다.
\( \Phi (x,y) = \frac{\Phi_{1}+\Phi_{2} } {2} y + \frac { \Phi_{1} – \Phi_{2}} { 2} \)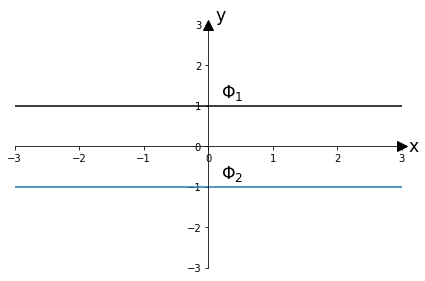
Fig a
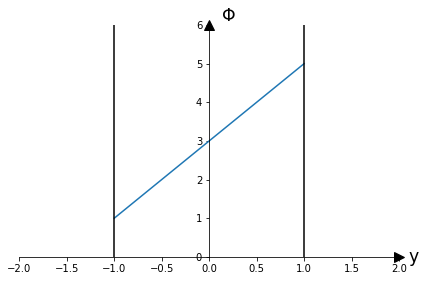
각각의 electric potential을 y=1의 위치에서 \( \Phi_{1}=5V \) y=-1위치에서 \( \Phi_{2}=1V\)이라고 값을 결정해본다면 \( \Phi(x,y)= 2y+3\)의 관계식을 보여준다. 이는 전기장 내에서의 어떤 지점에서의 전위가 되며 그래프로 그려보면 Fig b와 같이 그려볼 수 있다.